Counting In Binary On Your Hands

Counting to 31 using 1 hand and counting to 1023 using 2 hands

10 Fingers and 10 Toes

When a kid turns 10, we joke with them that they’ve run out of fingers to count their age, and next year, they’ll have to use their toes.

That scheme will last them until they are 20, and then they’ll be too old to count their age on their fingers.

Base 10

So, counting their age on their hands involves using base 10 because they have 10 fingers.

If your kid has seen math all the way to place values, they’ll know about numbers in each place value going from 0 to 9.

For example, the max number with three place values: _ _ _ is 999, and the lowest number is 0.

Each place value represents 10 to a power
- The first-place value is 10^0
- The second-place value is 10^1
- The third-place value is 10^2
- so on and so forth

As an example, we can represent 987 as follows:
=> 9 *10^2 + 8*10^1 + 7*10^0
=> 9*100 + 8*10 + 7*1
=> 900 + 80 + 7
=> 987

Using both hands to count using base 10 means that a full place value is their hands and a full place value is their feet.

Hands can count up to 10.

Hands and Feet can count up to 20.

There isn’t a way to represent a place value with each finger, so they/we are limited to counting to twenty.

Base 2 - Binary

If we did want to represent a place value with each finger, we would be limited to each finger being “up” or “down.”

Luckily, there is a number system where each place value only has two states (up or down).

That number system is the base 2 number system, also commonly called binary.

The idea behind base 2 (also called binary) is that each place value can only have a value of 0 or 1

• 0 is 0

• 1 is 1

• 2 is 10

• 3 is 11

Each place value represents 2 to a power
- The first-place value is 2^0
- The second-place value is 2^1
- The third-place value is 2^2
- so on and so forth

So when we write the number 3 (base 10) as 11 (base 2), we are saying:
=> 1*2^1 + 1*2^0
=> 1*2 + 1*1
=> 2 + 1
=> 3

If we have 5 place values in binary, we have
- 2^0 (1)
- 2^1 (2)
- 2^2 (4)
- 2^3 (8)
- 2^4 (16)

This means we can add any combination of 1, 2, 4, 8, or 16 to represent a number using those place values.

For example, to represent 20, we would use one 16 and one 4:
=> _____
=> 10100
=> 1*2^4 + 0*2^3 + 1*2^2 + 0*2^1 + 0*2^0
=> 1*16 + 0*8 + 1*4 + 0*2 + 0*1
=> 16 + 0 + 4 + 0 + 0
=> 20

5 Fingers

Speaking of fingers (going back to the beginning), we have 5 fingers in one hand!

This means that each finger can represent a place value in the binary system.

So now we can count with our fingers so that each finger represents a power of 2.

__0__

__1__

__2__

__4__

__8__

__16__

We can then use a combination of the digits to count up.

5-digit binary number

If we use up all our fingers on one hand, we get the binary number:
11111
=> 1*2^4 +1*2^3 + 1*2^2 +1*2^1 + 1*2^0
=> 1*16 + 1*8 + 1*4 + 1*2 + 1*1
=> 16 + 8 + 4 + 2 + 1
=> 24 + 4 + 2 + 1
=> 28 + 2 + 1
=> 30 + 1
=> 31

This means that we can use 1 of our hands to count up to 31 now instead of just 5.

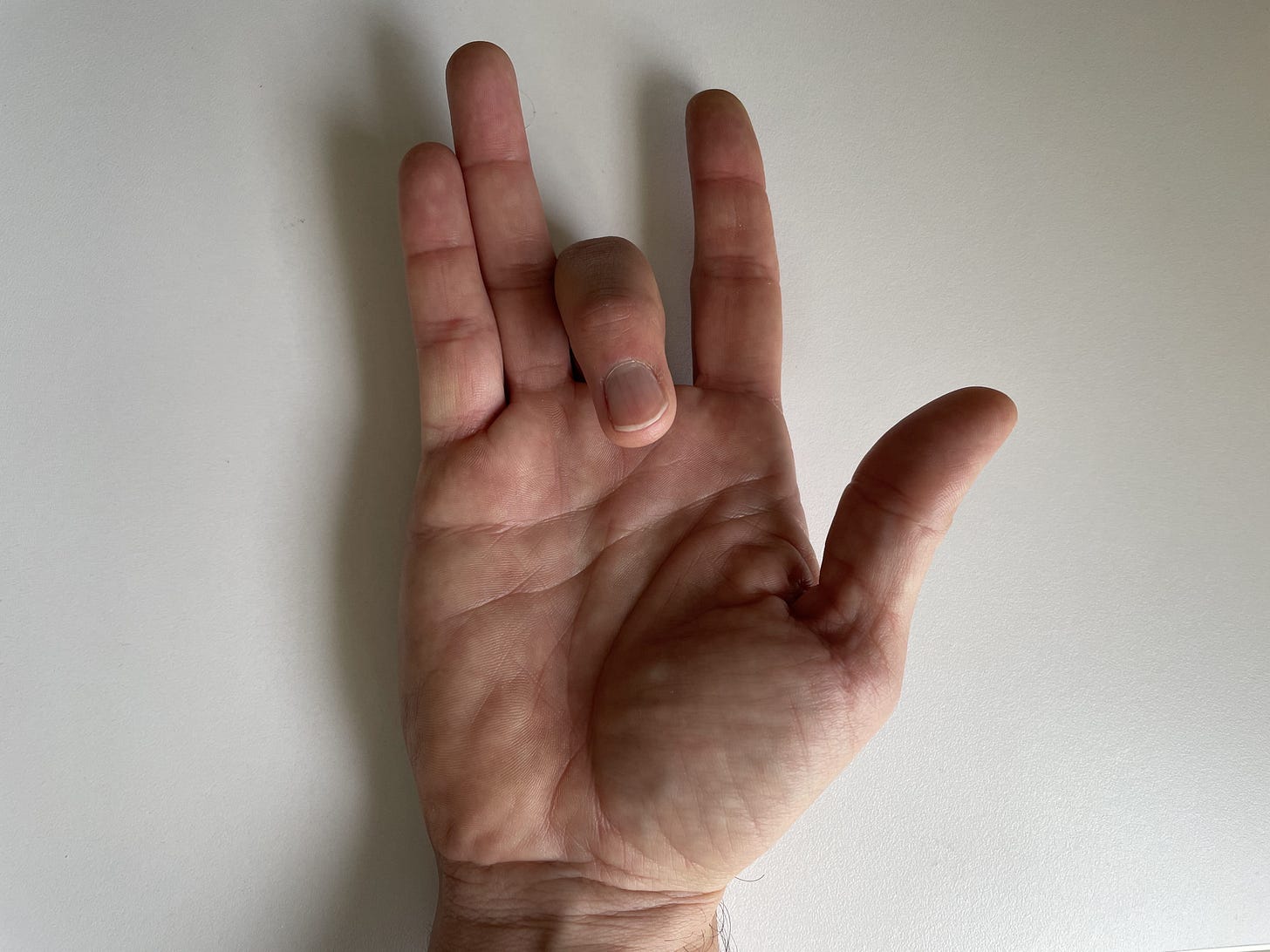
As an example, here’s a binary number represented on the fingers of my hand:

This can be written in binary as
11011
=> 1*2^4 +1*2^3 + 0*2^2 +1*2^1 + 1*2^0
=> 1*16 + 1*8 + 0*4 + 1*2 + 1*1
=> 16 + 8 + 0 + 2 + 1
=> 24 + 0 + 2 + 1
=> 24 + 2 + 1
=> 26 + 1
=> 27

Counting to 31 using 1 hand

Here’s a video of me counting to 31 in one hand using my fingers as binary place value representations:

Counting to 1023 using 2 hands

With 2 hands, we have 10 place values to have a zero or 1.

So the biggest number we can represent using our hands in binary is:

Right Hand Left Hand
11111 11111
=> 1*2^9 +1*2^8 + 1*2^7 +1*2^6 + 1*2^5 + 1*2^4 +1*2^3 + 1*2^2 +1*2^1 + 1*2^0
=> 1*512 + 1*256 + 1*128 + 1*64 + 1*32 + 1*16 + 1*8 + 1*4 + 1*2 + 1*1
=> 512 + 256 + 128 + 64 + 32 + 16 + 8 + 4 + 2 + 1
=> 768 + 128 + 64 + 32 + 16 + 8 + 4 + 2 + 1
=> 896 + 64 + 32 + 16 + 8 + 4 + 2 + 1
=> 960 + 32 + 16 + 8 + 4 + 2 + 1
=> 992 + 16 + 8 + 4 + 2 + 1
=> 1008 + 8 + 4 + 2 + 1
=> 1016 + 4 + 2 + 1
=> 1020 + 2 + 1
=> 1022 + 1
=> 1023

I’ll save you the video of counting to 1023 using my fingers.

Next steps

Try teaching yourself and your kid how to count in binary using your hands.

You’ll find after a few days that it becomes easier and easier.

What has been tricky for our family is actually finding opportunities where we need to count all the way into the 20s, let alone the 30s.

Try it out and let me know how it went :)

Until next time,
Sebastian.

PS - Parent Consulting Circle for paid subscribers

One of the hardest things I/we found when we first started trying to help our kid was finding other math-kid parents we could reach out with questions to see what had worked, what hadn’t worked, and what they were doing now.

Starting today, I will be setting up weekly office hours where you can come and ask your questions about helping your math kid! All you need to do is become a paid subscriber ($8/month) and you’ll receive the information for next week’s session.

This is your chance to ask any questions you have and hear from other parents, too. It's okay if you're a little shy about asking - you can do it without anyone knowing it's you!

We will talk about all sorts of stuff that can help kids from ages 5 to 18 who are extra math-y or learn in their own special way. You’ll get to share your thoughts and hear from me/others about their math-kid-parent/guardian journey.

During the office hours, you'll learn:

• Tips on how to help your math kid.

• That you're not alone - other families are going through the same things.

• All the different ways your kid can grow up to be awesome.

• How the Family Services team can help you and your kid.

This meeting is just for parents and will be about 60 minutes long. You can come and stay for as short or as long as you like.

Don't forget to let us know you're coming so we can save you a spot and send you some helpful stuff after the meeting. Can't wait to see you there! 🌟